- Martin Mann, Mostafa M Mohamed, Syed M Ali, and Rolf Backofen
Interactive implementations of thermodynamics-based RNA structure and RNA-RNA interaction prediction approaches for example-driven teaching
PLOS Computational Biology, 14 (8), e1006341, 2018. - Martin Raden, Syed M Ali, Omer S Alkhnbashi, Anke Busch, Fabrizio Costa, Jason A Davis, Florian Eggenhofer, Rick Gelhausen, Jens Georg, Steffen Heyne, Michael Hiller, Kousik Kundu, Robert Kleinkauf, Steffen C Lott, Mostafa M Mohamed, Alexander Mattheis, Milad Miladi, Andreas S Richter, Sebastian Will, Joachim Wolff, Patrick R Wright, and Rolf Backofen
Freiburg RNA tools: a central online resource for RNA-focused research and teaching
Nucleic Acids Research, 46(W1), W25-W29, 2018.
Teaching - hybrid-only : max. intermol. bps source at github@BackofenLab/RNA-Playground
The identification of an optimal RNA-RNA interaction without consideration
of intramolecular base pairs can be done efficiently in $O(nm)$ time and space
for two RNA sequences $S^{1}$ and $S^{2}$ of lengths $n$ and $m$, resp.,
(Brian Tjaden et al., 2006).
For a Nussinov-like
interaction prediction, a dynamic programming table $H$ is filled via the
prefix-based recursion
Here, in order to prepare the computation of accessibility-based interaction prediction, the following interval-based recursion is used to identify the RNA-RNA interaction with the maximal number of intermolecular base pairs. To this end, the four-dimensional table $D$ is filled, where an entry $D^{i,k}_{j,l}$ represents the maximal number of base pairs for the sequence intervals $S^{1}_{i..k}$ and $\overleftarrow{S^{2}_{j..l}}$ under the condition that both interval ends are forming the intermolecular base pairs $(S^{1}_{i},\overleftarrow{S^{2}_{j}})$ and $(S^{1}_{k},\overleftarrow{S^{2}_{l}})$. A list of up to 15 maximal base pair RNA-RNA interactions is provided via exhaustive traceback for all table entries with maximal value, i.e. $D^{i,k}_{j,l}=\max(D)$.
$H_{i,j}=\max\begin{cases} H_{i-1,j-1}+1 & \text{if }S^{1}_{i}, \overleftarrow{S^{2}_{j}}\text{ compl. base pair}\\ H_{i-1,j} \\ H_{i,j-1} \end{cases}$,
where an entry $H_{i,j}$ provides the maximal number of intermolecular
base pairs for the prefixes $S^{1}_{1..i}$ and $\overleftarrow{S^{2}_{1..j}}$, the reverse sequence of $S^2$.
Note, this recursion is a variant of a global
Needleman-Wunsch (1970)
sequence alignment with special scoring, where only
Watson-Crick as well as GU base pairs are considered complementary and thus similiar.
A traceback from the entry $H_{i,j}$ with the highest value provides
an according optimal interaction.
Here, in order to prepare the computation of accessibility-based interaction prediction, the following interval-based recursion is used to identify the RNA-RNA interaction with the maximal number of intermolecular base pairs. To this end, the four-dimensional table $D$ is filled, where an entry $D^{i,k}_{j,l}$ represents the maximal number of base pairs for the sequence intervals $S^{1}_{i..k}$ and $\overleftarrow{S^{2}_{j..l}}$ under the condition that both interval ends are forming the intermolecular base pairs $(S^{1}_{i},\overleftarrow{S^{2}_{j}})$ and $(S^{1}_{k},\overleftarrow{S^{2}_{l}})$. A list of up to 15 maximal base pair RNA-RNA interactions is provided via exhaustive traceback for all table entries with maximal value, i.e. $D^{i,k}_{j,l}=\max(D)$.
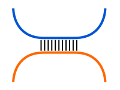
RNA sequence $S^{1}$:
RNA sequence $S^{2}$:
(Computation uses reversed sequence $\overleftarrow{S^2}$)
(Computation uses reversed sequence $\overleftarrow{S^2}$)
Visualization of interacting base pairs (selected structure)
Due to the four-dimensionality of $D$, we only list the optimal
hybrid structures (up to 15). On selection, the intermolecular base pairs are
visualized.
| Possible Structures |
|---|
Basepair number of selection:
The box provides an ASCII representation of the interacting
base pairs of the selected structure with $S^{1}$ on top and $\overleftarrow{S^{2}}$
on the bottom.
Note, sequence $S^{2}$ is reversed (running from right ($5'$-) to left
($3'$-end)) within this representation.
Note further, if no interacting
base pairs are present, no visualization is done.


