- Martin Mann, Mostafa M Mohamed, Syed M Ali, and Rolf Backofen
Interactive implementations of thermodynamics-based RNA structure and RNA-RNA interaction prediction approaches for example-driven teaching
PLOS Computational Biology, 14 (8), e1006341, 2018. - Martin Raden, Syed M Ali, Omer S Alkhnbashi, Anke Busch, Fabrizio Costa, Jason A Davis, Florian Eggenhofer, Rick Gelhausen, Jens Georg, Steffen Heyne, Michael Hiller, Kousik Kundu, Robert Kleinkauf, Steffen C Lott, Mostafa M Mohamed, Alexander Mattheis, Milad Miladi, Andreas S Richter, Sebastian Will, Joachim Wolff, Patrick R Wright, and Rolf Backofen
Freiburg RNA tools: a central online resource for RNA-focused research and teaching
Nucleic Acids Research, 46(W1), W25-W29, 2018.
Teaching - co-folding : linked prediction source at github@BackofenLab/RNA-Playground
To predict RNA-RNA interactions optimizing both intra- as well as
intermolecular base pairs one can use a so called co-folding approach.
Here, the two interacting sequences are concatenated (using a
non-pairing linker sequence) to a single pseudo-sequence
that is then folded via single structure prediction.
When using a full nearest-neighbor energy model, special care has
to be taken for the scoring of the loop containing the linker as discussed by
Ivo L. Hofacker and coworkers (1994).
Here, we extend the Nussinov algorithm for such a co-folding scheme. No special linker treatment is necessary, since we do a base pair maximization without taking the base pair's context into account. We can directly use the Nussinov algorithm without any extensions when using a linker sequence of length $l+1$ ($L=\text{X}_{1}..\text{X}_{l+1}$), where $l$ denotes the minimal loop length. The linker's length enables intermolecular base pairs between the concatenated sequence ends. Thus, for two sequences $S^{1}$ and $S^{2}$, the hybrid sequence used for folding is given by $S=S^{1}LS^{2}$.
For prediction, we fill the dynamic programming table $D$, where an entry $D_{i,j}$ provides the maximal number of base pairs of any nested structure for the subsequence from $S_{i}$ to $S_{j}$. The entry $D_{1,n}$ provides the overall maximal number of base pairs for the whole hybrid sequence $S$ of length $n=|S^{1}|+l+1+|S^{2}|$. Watson-Crick as well as GU base pairs are considered complementary.
Beside the identification of an according optimal hybrid structure via traceback (intra- and intermolecular base pairs are given by $()$ and $[\;]$, resp.), we provide an exhaustive enumeration of up to 15 suboptimal hybrids using the algorithm by Stefan Wuchty et al. (1999). For each structure, the according traceback is visualized on selection.
Here, we extend the Nussinov algorithm for such a co-folding scheme. No special linker treatment is necessary, since we do a base pair maximization without taking the base pair's context into account. We can directly use the Nussinov algorithm without any extensions when using a linker sequence of length $l+1$ ($L=\text{X}_{1}..\text{X}_{l+1}$), where $l$ denotes the minimal loop length. The linker's length enables intermolecular base pairs between the concatenated sequence ends. Thus, for two sequences $S^{1}$ and $S^{2}$, the hybrid sequence used for folding is given by $S=S^{1}LS^{2}$.
For prediction, we fill the dynamic programming table $D$, where an entry $D_{i,j}$ provides the maximal number of base pairs of any nested structure for the subsequence from $S_{i}$ to $S_{j}$. The entry $D_{1,n}$ provides the overall maximal number of base pairs for the whole hybrid sequence $S$ of length $n=|S^{1}|+l+1+|S^{2}|$. Watson-Crick as well as GU base pairs are considered complementary.
Beside the identification of an according optimal hybrid structure via traceback (intra- and intermolecular base pairs are given by $()$ and $[\;]$, resp.), we provide an exhaustive enumeration of up to 15 suboptimal hybrids using the algorithm by Stefan Wuchty et al. (1999). For each structure, the according traceback is visualized on selection.
RNA sequence $S^{1}$:
RNA sequence $S^{2}$:
Minimal loop length $l$:
Delta #bp to maximum:
Used recursion (Nussinov algorithm):
| Possible Structures |
|---|
Select a structure from the list or (multiple times) a cell of $D$
to see according tracebacks. Note, the structure list is limited to
the first 15 structures identified via traceback and thus depends
on the recursion case order.
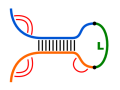
Below, we provide a graphical depiction of the selected hybrid structure. Note, the rendering does not support a minimal loop length of 0.
Below, we provide a graphical depiction of the selected hybrid structure. Note, the rendering does not support a minimal loop length of 0.
Visualization done with
forna.
Base pairs are given by red edges, the sequence backbone is given by
gray edges.
Visualization of interacting base pairs (selected structure)
The box provides an ASCII representation of the interacting
base pairs of the selected structure with $S^{1}$ on top and $S^{2}$
on the bottom.
Note, sequence $S^{2}$ is reversed (running from right ($5'$) to left
($3'$)) within this representation.
Note further, if no interacting
base pairs are present, no visualization is done.


