The problem of predicting the secondary structure of an RNA is called the RNA folding problem. Existing computational approaches are based on a thermodynamic model that gives a free energy value for each secondary structure. The structure with the lowest free energy (called the minimum free energy (mfe) structure) is expected to be the most stable one. Here, we consider the inverse RNA folding problem, which is the design of RNA sequences that fold into a desired structure. This design is applicable to cis-acting mRNA elements such as the iron responsive element (IRE) and the polyadenylation inhibition element (PIE). Both elements have conserved sequence positions in loops. Using the INFO-RNA web server, artificial cis-acting elements can be designed, which have a much higher folding probability compared to natural elements. Furthermore, the INFO-RNA web server is usable for the design of artificial microRNA (miRNA) precursors that are as stable as possible. Other potential application areas are the design of ribozymes and riboswitches, which may be used in research and medicine, and the design of noncoding RNAs, which are involved in a large variety of processes, e.g. gene regulation, chromosome replication, and RNA modification.

Given a set of base pairs, we aim at finding an RNA sequence that is going to adopt these pairs. Additionally, restrictions on the sequence level can be specified by constraints given in IUPAC ambiguity codes for nucleotides. These constraints can be relaxed by allowing some violations. Thereto, a maximal number of violations has to be specified and furthermore, positions where violations may occur have to be given.

Note: SECISDesign is not maintained anymore.
The source code is available at http://www.bioinf.uni-freiburg.de/Software/

• Anke Busch and Rolf Backofen
  INFO-RNA - A Server for Fast Inverse RNA Folding Satisfying Sequence Constraints
  Nucleic Acid Research, 35 (Web Server Issue) W310-3, 2007
  
• Anke Busch and Rolf Backofen
  INFO-RNA - a fast approach to inverse RNA folding
  Bioinformatics, 22 no. 15 pp. 1823-31, 2006
  
• Martin Raden, Syed M Ali, Omer S Alkhnbashi, Anke Busch, Fabrizio Costa, Jason A Davis, Florian Eggenhofer, Rick Gelhausen, Jens Georg, Steffen Heyne, Michael Hiller, Kousik Kundu, Robert Kleinkauf, Steffen C Lott, Mostafa M Mohamed, Alexander Mattheis, Milad Miladi, Andreas S Richter, Sebastian Will, Joachim Wolff, Patrick R Wright, and Rolf Backofen
  Freiburg RNA tools: a central online resource for RNA-focused research and teaching
  Nucleic Acids Research, 46(W1), W25-W29, 2018.
  

Results are computed with INFORNA version 2.2.0 linking Vienna RNA package 1.8.4

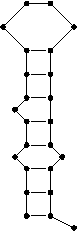
The RNA secondary structure, you wish to design a sequence for, has to be given in bracket notation.
A base pair between bases i and j is represented by a '(' at the ith position and a ')' at position j.
Unpaired bases are represented by dots. The folding temperature is fixed at 37C.

Example:

The following structure is represented by the string (((.((.(((....))))).))).

The parameter constraints are: String length has to be in range (5,300). Maximally 1 line is allowed.
Defaults to ()

Input Format

For each position you want to set a constraint, you have to give the position number, the IUPAC symbol you want to restrict this sequence position to, and a '+' or '-' for allowing the constraint to be violated or not.

Example:

				 4 C -
				 7 Y -
				 9 C +
				10 G +
				15 C +
				16 G -
				20 C -
				

For further information see Sequence Constraints and Constraint Violations.

Sequence Constraints

If you want positions of the desired sequence to be fixed to a special base or restricted to some bases,
these constraints can be given by IUPAC ambiguity codes for nucleotides, where

	A	→	A
	C	→	C
	G	→	G
	T/U	→	U
	M	→	A or C
	R	→	A or G
	W	→	A or U
	S	→	C or G
	Y	→	C or U
	K	→	G or U
	V	→	A or C or G
	H	→	A or C or U
	D	→	A or G or U
	B	→	C or G or U
	N	→	A or C or G or U

Example:

The Structure	(((.((.(((....))))).))).
is constrained by	C  Y CG    CG   C

Hints about the input format can be found here .

Constraint Violations

Furthermore, you can allow some violations of the constraints. All constrained positions have to be marked with either a '+' or a '-', where

	+	→	means that the constraint at this position is allowed to be violated.
	-	→	means that the constraint at this position is strict and thus not allowed to be violated.

Example:

The Structure	(((.((.(((....))))).))).
is constrained by	C  Y CG    CG   C
Allowed violations	-  - ++    ++   -

Hints about the input format can be found here .

If you do not want to accept constraint violations at all positions where you have allowed them, but you want to tolerate violations up to a given total number, you can fix this number here.

Example: (same as above)

Assume you have given the following structure, sequence constraints, and allowed positions where the constraints can be violated:

structure	(((.((.(((....))))).))).
sequence constraints	GGGGCCGCCC    GGGGGGCCCA
allowed violations of the constraints	--+-+++---    ---++-+---

If you fix the maximal number of constraint violations in the designed sequence to 3, the constraints are allowed to be not fulfilled on at most 3 positions (out of the 7 positions, where violations are allowed at all).

The parameter constraints are: Input value has to be parsable as Integer.
Defaults to (999)

During the SLS, an objective function is needed to increase the folding probability of the mRNA sequence. One of the following functions or combinations of them can be chosen:

	mfe:	Minimizing the distance of the minimum-free-energy-structure of the designed sequence and the wanted structure.
	prob:	Maximizing the probability of the designed sequence folding into the wanted structure. (Since this function is quite time consuming, it is just available for structures with lengths smaller or equal to 200.)

During the SLS, mutations to sequence neighbors* that have an minimum free energy (mfe) structure with a smaller distance to the target structure than the current one are always approved. Furthermore, the SLS is allowed to move to worse neighbors with a fixed probability for accepting bad mutations to overcome local optima (sequences which are better than all their neighbors but not necessarily the globally best solution). A tested neighbor is always retained if it has an mfe structure that has a smaller distance to the target one than the current sequence. Otherwise, it is kept with the fixed probability.

The parameter constraints are: Input value has to be parsable as Double. The value must be greater than or equal to 0 and must be smaller than or equal to 1.
Defaults to (0.1)

The order, in which the neighbors* of a sequence are tested, can be chosen arbitrarily or depending on a kind of look-ahead of one selection step. Thereto, candidates are evaluated with an additional energy-based criterion and pre-sorted for mutation. After fixing this test order of the neighbors, they are evaluated concerning the actual optimization criterion of minimizing the structure distance of the mfe structure of the sequence and the target structure.

* A sequence neighbor of a sequence is another sequence that differentiates from it either in one base pair or in an unbound position.

The server can design several sequences for you (up to 50 sequences in single run). The Number of Designed Sequences specifies this number. Please note, if you want the server to design more than a single sequence, you have to choose the email option below since the computation can last some minutes.

Please be aware that the designed sequences of a single run might be very similar, which is due to the rather fixed initializing sequence.

The parameter constraints are: Input value has to be parsable as Integer. The value must be greater than or equal to 1 and must be smaller than or equal to 50.
Defaults to (1)

Design of a long hairpin loop with soft and hard sequence constraints

The example's result can be directly accessed here